Number Theory I¶
References:
- [GCAC] A Graduate Course in Applied Cryptography, Dan Boneh and Victor Shoup
- [CINTA] A Computational Introduction to Number Theory and Algebra, Victor Shoup
- [HAC] Handbook of Applied Cryptography, Alfred J. Menezes, Paul C. van Oorschot and Scott A. Vanstone
- [ITMC] Introduction to Modern Cryptography, Jonathan Katz and Yehuda Lindell (3rd Edition)
- Elementary number theory in sage
Dependencies:
This notebook uses sage math as kernel
import sage.misc.banner # sage math version info
rchars = "┘─│┐┌└"
smallbanner = sage.misc.banner.banner_text(full=True)
for c in rchars:
smallbanner = smallbanner.replace(c,"") # remove ascii art box
print(smallbanner)
#banner() # full banner with box
SageMath version 9.5, Release Date: 2022-01-30 Using Python 3.10.12. Type "help()" for help.
Number systems¶
Natural Numbers < Integers < Rational numbers < Real nunmbers
For cryptographic applications only (subsets of) the integers are important
Integers¶
Possible notations:
- integers: $$ \mathbb{Z} = \{ \dots, -2, -1, 0, 1, 2, \dots \} $$
- non-zero integers: $$ \mathbb{Z}^{\neq} = \mathbb{Z}^{*} = \{ \dots, -2, -1, 1, 2, \dots \} $$
- positive integers: $$ \mathbb{Z}^+ = \mathbb{Z}_+ = \mathbb{Z}^> = \{ 1, 2, \dots \} $$
- non-negative integers: $$ \mathbb{Z}^{0+} = \mathbb{Z}^\geq = \{ 0,1, 2, \dots \} $$
Natural Numbers¶
Also referred to as non-negative integers or positive integers if without $ 0 $. Possible notations:
- non-negative integers including zero: $$ \mathbb{N} = \mathbb{N}_0 = \{0,1,2,3,\dots\} $$
- positive integers: $$ \mathbb{N} = \mathbb{N}_1 = \mathbb{N}^* = \{1,2,3,\dots\} $$
Every positive integer is either composite, prime, or the unit $ 1 $
Natural Numbers in sage¶
N = NonNegativeIntegers(); N # Includes 0
Non negative integers
-1 not in N and 0 in N
True
N_1 = PositiveIntegers(); N_1 # Excludes 0
Positive integers
-1 not in N_1 and 0 not in N_1
True
Divisability¶
- If $ a, b \in \mathbb{Z}$ and $ a \; divides \; b $, written as $ a | b $, then there exists a $ c \in \mathbb{Z} $ such that $ ac = b $.
- If $ a $ does not divide $ b $, we write $ a \nmid b $
- If $ a | b $ and $ a | c $, then $ a | (Xb + Xc)$ for any $ X,Y \in \mathbb{Z}$
- If $ a | b $ and $ a $ is positive, $ a $ is called a $ divisor $ of $ b $
- If $ a \notin \{ 1, b \} $ then it is a nontrivial divisor or factor of $ b $
- A positive integer $ p > 1 $ is prime if it has no factors, so that his only divisors are $ 1 $ and itself.
- A positive integer that is not prime is called composite
- Per convention $ 1 $ is neither prime nor composite but called unit
Divisability in sage¶
a = 3; b = 12
a.divides(b)
True
b % a == 0
True
a = 5; b = 12
a.divides(b)
False
b % a == 0
False
Prime numbers¶
A prime is a natural number greater than $ 1 $ that is only divisible by $ 1 $ and itself. A natural number greater than $ 1 $ that is not prime is called composite number.
$ \mathbb{P} =\{2,3,5,7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,... \}$
Open questions¶
Several historical questions regarding prime numbers are still unsolved.
These include Goldbach's conjecture, that every even integer greater than 2 can be expressed as the sum of two primes, and the twin prime conjecture, that there are infinitely many pairs of primes having just one even number between them.
Primes in sage¶
See also sage documentation on primes
P = Primes(); P # define set of all primes in sage
Set of all prime numbers: 2, 3, 5, 7, ...
P.cardinality()
+Infinity
primes_first_n(14)
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43]
P.next(10) # get the next prime after the given number
11
# get a random 32 bit prime specified as beeing between lbound and n
random_prime(n=2**32-1,proof=True,lbound=2**31)
3031999013
Primality test¶
The test if a given number is prime is called primality test.
A simple inefficient primality test (and factorization algorithm) is trial division: Given an input number $ a $, check whether it is divisible by $ 2 $ or any odd number between $ 2 $ and $\sqrt {a}$. If so, it is not prime and this number is one of its factors.
If we are only interested in the question if the number is prime or not, there are deterministic tests which run in polynomial time (e.g., AKS primality test).
There are also probabilistic tests which are even faster but have small (configurable) error probability. Usually they never report a prime as a composite number, but it is possible that certain composite numbers are reported as prime.
11 in P # check if number is prime in sage
True
10 in P
Primality testing¶
def isPrime_sage(n) -> bool:
""" wrapper function for primality tests in sage """
return n in Primes(True)
def isPrime_sage_BailiePSW(n) -> bool:
""" wrapper function for that uses PARI's Baillie-PSW probabilistic primality test """
return Integer(n).is_pseudoprime()
import gmpy2
def isPrime_python_gmpy2(n) -> bool:
""" primality test in python using gmpy2 uses Miller-Rabin test
https://gmpy2.readthedocs.io/en/latest/mpz.html#gmpy2.is_prime
"""
return gmpy2.is_prime(int(n)) # has to be python int()
Primality testing¶
%time isPrime_trial_division(random_number) # 32 bit random_number
CPU times: user 846 ms, sys: 0 ns, total: 846 ms Wall time: 844 ms
(False, [3, 5, 67, 2136833])
%time isPrime_sage(random_number)
CPU times: user 53 µs, sys: 12 µs, total: 65 µs Wall time: 74.9 µs
False
%time isPrime_python_gmpy2(random_number)
CPU times: user 0 ns, sys: 461 µs, total: 461 µs Wall time: 7.18 ms
False
Note that, testing if a given positive integer is prime is resonably fast
Factorization¶
Factorization is thought to be a computationally difficult problem (i.e., no polynomial-time algorithm for factoring has been demonstrated). Primality testing is comparatively easy.
- Fundamental theorem of arithmetic: every natural number greater than $ 1 $ is either a prime itself or can be factorized as a product of primes that is unique up to their order (ie., the order is not relevant)
factor(12) # prime factors of a composite number
2^2 * 3
factor(5) # prime factor of a prime
5
In sage quadratic sieve (qsieve) is a more efficient factorization algorithm. It is the second-fastest known method after the general number field sieve (i.e., the time complexity is sub-exponential but still not polynomial).
print(next_prime(2^80),next_prime(2^81)) # sample two 2^80 bit primes
1208925819614629174706189 2417851639229258349412369
%time qsieve(next_prime(2^80) * next_prime(2^81)) # factor the product
CPU times: user 6.59 ms, sys: 237 µs, total: 6.83 ms Wall time: 703 ms
([1208925819614629174706189, 2417851639229258349412369], '')
Modulo arithmetic¶
The notation $ a \mod N $ denotes the remainder of $ a $ upon division by $ N $.
6*3 % 15 # modulo operation in python
3
mod(6*3,15) # modulo function in sage
3
Exponentiation (power of) some value modulo $ n $ e.g., $ 2^4 \mod 15 $
2**4
16
# python build in
pow(2,4,15)
1
Integers modulo $n$¶
- set of integers modulo $n$: $$ \mathbb{Z}_n=\{0,1,2,...,n-1\} $$
- sometimes also denoted as $ \mathbb{Z}/n\mathbb{Z} $, which stands for $ \mathbb{Z} $ without all multiples of $ n $
Example: If $n=15$ then $ \mathbb{Z}_n=\{0,1,2,4,5,6,7,8,9,10,11,12,13,14\} $
Zn = IntegerModRing(15); Zn
Ring of integers modulo 15
Zn.list() # list all elements
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]
Zn.order() # number of elements
15
Integers modulo $n$¶
Zn.list() # list all elements where n=15
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]
6*3 # result in the set of integers
18
Zn(6*3) # result in the set of integers mod n
3
Zn.random_element()
9
Greatest common divisor (GCD)¶
$$ \begin{align*} \frac{divident}{divisor} &= quotient \\ \; \\ divident &= quotient \cdot divisor + remainder \end{align*} $$
The greatest common divisor (gcd) of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers.
number_of_divisors(12) # the number of divisors of a number
6
divisors(12) # list of divisors of a number
[1, 2, 3, 4, 6, 12]
divisors(9)
[1, 3, 9]
gcd(12,9) # sage gcd
3
Euclidean algorithm¶
The Euclidean algorithm is an efficient method for computing the greatest common divisor (GCD) of two numbers.
The basic principle is that replacing the larger of the two numbers by its difference with the smaller number does not change the greatest common divisor. This process is reapeated until the remainder is $ 0 $. The last non-zero difference is the gcd.
The following is a visual example of computing the gcd of $ 49 $ (black) and $ 21 $ (red), which is $ 7 $.
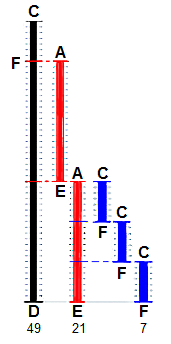
Euclidean algorithm example¶
def euclide(a, b,verbose=False):
""" euclidean algorithm as a recursive function """
assert a >= b,"a must be larger than b"
if verbose: print(f"a = {a:3} b = {b:3}")
if b == 0:
return a
else:
return euclide(b, a % b,verbose)
euclide(12,9,True)
a = 12 b = 9 a = 9 b = 3 a = 3 b = 0
3
Relatively prime (coprime)¶
If $gcd(a,b)=1$ then $a$ and $b$ are called relatively prime or coprime.
Neither $ a $ or $ b $ has to be prime in order for them to be relatively prime to each other. One example would be $ 8 $ and $ 9 $.
gcd(8,9)
1
8 not in P and 9 not in P
True
Relatively prime (coprime)¶
If either $ a $ or $ b $ is prime, then they might, or might not be relatively prime to each other:
- All integers from $ 1 $ to $ p \in \textrm{Primes}$ have to be relatively prime to $ p $
- There might be an integer $ z > p $ of which $ p $ is a prime factor. In this case $ z $ and $ p $ are not relatively prime
For example, $ 4 $ and $ 5 $ are coprime, whereas $ 10 $ and $ 5 $ are not coprime.
gcd(4,5)
1
gcd(10,5)
5
5 in P and 10 not in P
True
Question: If both numbers $a$,$b$ are prime, are they relatively prime to each other?
The answers is of course yes, since per definition of a prime they cannot have a common divisor, i.e., $\gcd(a,b) = 1 $
# example 5 and 3
assert 5 in P and 3 in P
gcd(5,3)
1
Some important properties of coprime numbers¶
If $\gcd(a,b) = 1 $ then:
- No prime number divides both $ a $ and $ b $
- There exist integers $ x,y $ such that $ ax + by = \gcd(a,b) = 1 $ (Bézout's identity representing the gcd is one in this case)
- The integer $ a $ has a multiplicative inverse ($x$) modulo $ b $
- The integer $ b $ has a multiplicative inverse ($y$) modulo $ a $
Modular multiplicative inverses¶
An element $ x \in \mathbb{Z}_n $ is invertible iff $ \gcd(x,n) = 1 $ i.e., there exists an element $ x^{-1} $ s.t., $ x \cdot x^{-1} = 1 \pmod{n} $.
This value $x^{-1}$ is called the modular multiplicative inverse of $ x $.
Examples:
- In $ \mathbb{Q} $ the inverse of $ 3 $ would be $ 1/3 $ since $ 3 \cdot 1/3 = 1 $.
- In $ \mathbb{Z}_n $ the inverse of $ 2 $ would be $ \frac{n+1}{2} $ since $ 2 \cdot \frac{n+1}{2} = n + 1 = 1 \pmod{n} $
A set where very element has an inverse¶
A subset of the set of integers modulo $n$, in which all elements are coprime (relatively prime) to $n$ is defined as:
$$ \mathbb{Z}^*_n = \{ x \in \mathbb{Z}_n : \gcd(x,n)=1 \} $$
The set $ \mathbb{Z}_n^* $ forms a group under mutliplication, hence the $^*$ symbol (see definition of a group for more details)
To construct this set all elements in $ \mathbb{Z}_n $ that are not invertible have to be eliminated. This includes $ 0 $ as it does not have an inverse.
Example:
If $n=15$ then $ \mathbb{Z}^*_n = \{ 1,2,4,7,8,11,13,14 \} $ and the order is $ | \mathbb{Z}^*_n | = 8 $
For small $n$, this set can be computed by iterating through the elements of $\mathbb{Z}_n$ and check if $\gcd(x,n) = 1 $. This is computationally inveasable for large $n$, but computing a multiplicative inverse of an element $ x \in \mathbb{Z}_n $, where $ \gcd(x,n) = 1 $ can be done in polynomial time, for example by using the extended Euclidean algorithm.
Extended Euclidean algorithm¶
The extended Euclidean is an extension to the Euclidean algorithm which computes the gcd of $ a $ and $ b $, as well as the coefficients of Bézout's identity, which are the integers $ x $ and $ y $ such that:
$$ ax + by = \gcd(a,b) $$
If $ a $ and $ b $ are coprime, i.e., $\gcd(a,b)=1$, then $ x $ is the modular multiplicative inverse of $ a \mod b $ and $ y $ is the modular multiplicative inverse of $ b \mod a $.
# exteneded euclidean algorithm in sage
xgcd(2,15) # returns (gcd,x,y)
(1, -7, 1)
mod(-7,15) # compute x mod b to get the inverse of a mod b
8
# compute the inverse of a mod b directly in sage
inverse_mod(2,15)
8
Extended Euclidean algorithm complexity¶
The extended euclidean algorithm can be used to compute the modular multiplicative inverse of $ a \mod b $ in polynomial time. In big $\mathcal{O}$ notation this algorithm runs in time $\mathcal{O}(\log_2(b))$ (assuming $a$ < $b$).
Euler's totient function $\varphi(n)$¶
Eulers totient function, written as $\varphi(n)$ or $\phi(n)$, gives the count of integers that are relatively prime to $n$. This resembles the number of invertable elements in $ \mathbb{Z}_n $, i.e., elements that have an inverse in $\mathbb{Z}_n$.
To compute the function the prime factors of $n$ need to be known!
If there are $ r $ different prime factors of $ n $, the function $ \varphi(n) $ can be computed as follows: $$ \varphi(n) = n \cdot \prod_{i=1}^{r} \left (1 - \frac{1}{p_i} \right ) $$
Example:
- $ \varphi(20)= \varphi(2^2 \cdot 5) = 20 \cdot (1-\frac{1}{2}) \cdot (1-\frac{1}{5}) = 20 \cdot \frac{1}{2} \cdot \frac{4}{5} = 8 $
euler_phi(20) # Eulers totient function in sage
8
Euler's totient function when $n \in \textrm{Primes}$¶
If $n=p \in \textrm{Primes}$ this implies that the group of elements in $\mathbb{Z}_p$ which have a multiplicative inverse modulo $ p $, i.e., the group $\mathbb{Z}^*_p$, has $p-1$ elements, i.e., $|\mathbb{Z}^*_p|=p-1$ since:
- all integers from $1$ to $p$ have to be relatively prime to $p$, the only exeception is $0$, since $gcd(0,p)=0$. Therefore this element needs to be removed.
- for all other numbers in the set it holds that, per defintion of a prime number it is not devisable by any other number than 1. $$ \mathbb{Z}^*_p = \mathbb{Z}_p / \{0\} = \{1,2,...,p-1\} \qquad \textrm{if } n \in \textrm{Primes} $$
In other words: Despite $0$ every other element in $\mathbb{Z}_p$ is invertable
Example: If $N=7$ then $ \mathbb{Z}^*_p = \{ 1,2,3,4,5,6,7 \} $
euler_phi(7)
6
Visualization of Euler's totient function when $n \in \textrm{Primes}$¶
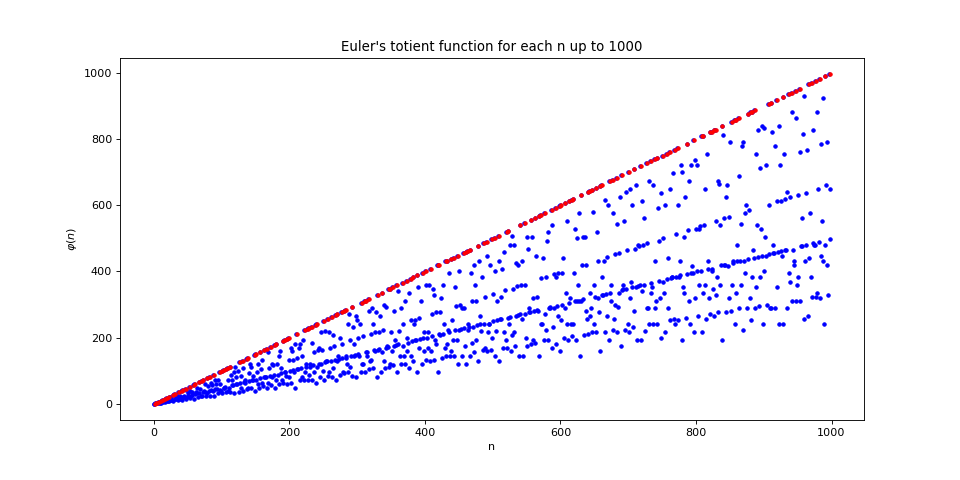
Phi of n, when n is prime the dot is colored red
Euler's totient function when $n=pq$ and $p,q \in \textrm{Primes}$¶
If $n$ is a product of two distinct primes $p$ and $q$, then the number of elements in $\mathbb{Z}_n^*$, denoted by $|\mathbb{Z}^*_n|$, is given by: $$ \begin{align*} \varphi(n)&=(p-1)(q-1) \\ \end{align*} $$
- In this case $p$ and $q$ are approx. the size of $\sqrt{n}$, i.e., $p,q \approx \sqrt{n}$
- In this case also $\varphi(n)$ is close to the size of $n$ since $$ \begin{align*} \varphi(n) &= (p-1)(q-1) \\ &= n - p - q + 1 \\ &\approx n - 2 \cdot \sqrt{n} \\ &\approx n \end{align*} $$
- Therefore if you pick a random element in in $\mathbb{Z}_n$, where $n=pq$ and $p,q \in \textrm{Primes}$ it is very likely to be invertable.
Euler's totient function when $n=pq$ and $p,q \in \textrm{Primes}$¶
Examples:
If $p=3$ and $q=5$ then $n=15$ and $ \mathbb{Z}^*_n = \{ 1,2,4,7,8,11,13,14 \} $ and $|\mathbb{Z}^*_n| = 8 $
# other larger example:
p=1009; assert p in Primes();
q=1013; assert q in Primes();
n=p*q; print(f"n = {n}")
n = 1022117
n not in Primes()
True
assert euler_phi(n) == (p-1)*(q-1) # Number of invertable elements $\varphi(n)$
(p-1)*(q-1) # almost as large as n
1020096
Visualization of Euler's totient function when $n = pq$ and $p,q \in \textrm{Primes}$¶
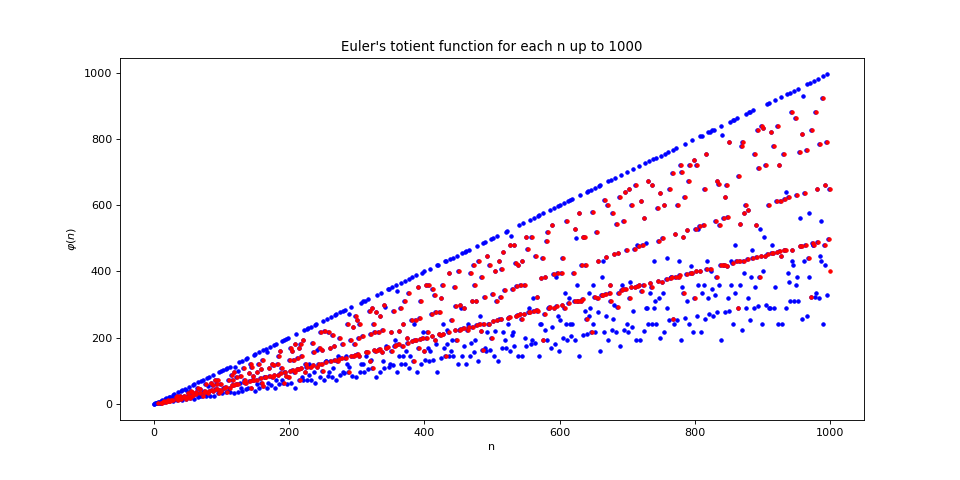
Phi of n, when n is the product of two primes the dot is colored red
Group¶
DEFINITION: Group (according to [ITMC]):
A group is a set $ \mathbb{G} $ along with a binary operation $ \circ $ for the the following conditions hold:
- Closure: For all $g,h \in \mathbb{G}, g \circ h \in \mathbb{G} $
- Existence of an idenity: There exists and identity $ e \in \mathbb{G} $ such that for all $ g \in \mathbb{G}, e \circ g = g = g \circ e $
- Existence of inverse: For all $ g \in \mathbb{G} $ there exists an element $ h \in \mathbb{G} $ such that $ g \circ h = e = h \circ g $. Such an $ h $ is called and inverse of $ g $.
- Associativity: For all $ g_1,g_2,g_3 \in \mathbb{G}, (g_1 \circ g_2) \circ g_3 = g_1 \circ (g_2 \circ g_3)$
A group $ \mathbb{G} $ with operation $\circ$ is abelian if the follwing holds:
- Commutativity: For all $ g,h \in \mathbb{G}$, $g \circ h = h \circ g $
When $ \mathbb{G} $ has a finite number of elements, we say $ \mathbb{G} $ is finite and let $ | \mathbb{G} | $ denote the order of the group i.e., the number of elements in $ \mathbb{G} $.
If $ \mathbb{G} $ is a group, a set $ \mathbb{H} \subseteq \mathbb{G}$ is a subgroup of $ \mathbb{G} $ if $ \mathbb{ H } $ iteself forms a group under the same operation associated with $ \mathbb{G} $. Every group $ \mathbb{G} $ has the trivial subgroups $ \mathbb{G} $ and $ \{e\} $.
Additive and multiplicative notation for the group operation $\circ$¶
Additive notation:
- group operation with two elements $ g + h $
- identity: $ 0 $
- inverse of element $g$ is given by $ -g $
Multiplicative notation:
- group operation with two elements $ g \cdot h $ or $ gh $
- identity: $ 1 $
- inverse of element $g$ is given by $ g^{-1} $ or $ 1/g $ or $ h/g $ instead of $ hg^{-1} $
Properties of groups¶
- A group is called cyclic, if there is a generator $g \in G$, such that for each $x \in G$, there is an integer $i$ where $x=g^i$.
- The order of a finite group is the number of its elements i.e., $|G|$.
- A group is called finite, if $|G|$ (its order) is finite.
- The order of a element $a$ of the group is the smallest integer $r$ such that, $a^r=e$ where $e$ is defined as identity element of the group. If no such $r$ exists the element $a$ has an infinite order.
Examples for groups¶
- The set of integers $\mathbb{Z}$ with the operation of addition ($+$), where the identity element would be $e=0$ and the inverse of an element would be the negative integer.
- This set is a abelian group with infinite order.
# Closure example:
g=3; h=7 # some elements in Z
g in Z and h in Z and g+h in Z
True
# Idenity example:
g=3; e=0 # identity element
e + g == g == g + e
True
# Inverse example:
g=3; _g=-3 # inverse of g
g + _g == e == _g + g
True
# Associativity example:
g1=3; g2=7; g3=23
(g1 + g2) + g3 == g1 + (g2 + g3)
True
# Commutativity example:
g=3; h=7
g + h == h + g
True
Examples for groups¶
- The set set of integers modulo $ n $, i.e., $ \mathbb{Z}_n $, where $ n > 1 $, is a abelian group under the operation of addition ($+$) modulo $ n $, i.e., $ a + b := [ a + b \mod n ] $. This group can also be denoted as $\mathbb{Z}^+_n $. The order of this group is $ n $, with the elements $ \{ 0, ..., n - 1 \} $. The inverse of any element $ a $ is $ [(n-a) \mod n] $
n=15; Zn = Integers(n); Zn
Ring of integers modulo 15
print(f"Z_n order = {Zn.order()}\nZ_n list = {Zn.list()}")
Z_n order = 15 Z_n list = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]
g = Zn.random_element(); h = Zn.random_element()
print(f"g = {g}; h = {h}")
g = 0; h = 6
# Closure example:
g = Zn.random_element(); h = Zn.random_element()
g in Zn and h in Zn and g+h in Zn
True
# Idenity element 0 in Zn under addition:
g = Zn.random_element(); e=Zn(0)
e + g == g == g + e
True
# Inverse of g mod n under addition is always n-g = g^-1
# as g + (n-g) mod n = 0
g = Zn.random_element(); _g=Zn(n-g) # inverse of g mod n
g + _g == e == _g + g
True
# Associativity example:
g1=Zn.random_element(); g2=Zn.random_element(); g3=Zn.random_element()
(g1 + g2) + g3 == g1 + (g2 + g3)
True
# Commutativity example:
g = Zn.random_element(); h = Zn.random_element()
g + h == h + g
True
Examples for groups¶
- $ \mathbb{Z}_n^* $ is not a group with operation $ a \cdot b \mod n $ being multiplication modulo $ n $, where $ n \notin \textrm{Primes}$.
- The identity element would be $e=1$, but not every element has an modular multiplicative inverse, e.g., $ 2 $ has no inverse in the integers, as $ 2 \cdot \frac{1}{2} = 1 $, but $\frac{1}{2} \notin \mathbb{Z}$ and hence not in $ \mathbb{Z}_n^* $.
# Z_n has n elements
n=15; Zn = Zmod(n)
print(f"{Zn.list()} len = {Zn.order()}")
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14] len = 15
# but not every element has a modulo multiplicative inverse mod n
Zn_unit = Zn.unit_group() # Zn_unit only has invertable elements (aka. units)
#print(type(Zn_unit))
print(f"{Zn_unit.list()} len = {Zn_unit.order()}") # show list of elements as represented by generators
print(f"(f0,f1) = {Zn_unit.gens_values()}") # show values of generators
(1, f1, f1^2, f1^3, f0, f0*f1, f0*f1^2, f0*f1^3) len = 8 (f0,f1) = (11, 7)
Finite Field¶
DEFINITION: Finite Field (according to [ITMC]):
A finite field (or Galois field), is a finite set $\mathbb{F}$ along with two binary operations $\{+,\cdot\} $ for which the following hold:
- $\mathbb{F}$ is a abelian group with respect to the operation $+$ and the idenity element, denoted as $ 0 $, for this group.
- The additive inverse of $ a \in \mathbb{F}$, denoted by $ -a $, is the unique element statisfying $ a + (-a) = 0 $.
- We can also write $b-a$ in place of $b+(-a)$.
- $\mathbb{F} \setminus \{0\}$ is an abelian group with respect to the operation $\cdot$ and the identity element, denoted as $ 1 $, for this group.
- The multiplicative inverse of $ a \in \mathbb{F}$, denoted by $a^{-1}$, is the unique element statisfying $a\cdot a^{-1} = 1 $.
- We can also write $b/a$ in place of $b\cdot a^{-1}=1$.
- We can also write $ab$ in place of $a \cdot b$.
- Distributivity: For all $a,b,c \in \mathbb{F}$ we have $ a \cdot (b+c) = a\cdot b + a\cdot c$
Properties of finite fields¶
- The number of elements of a finite field is called its order.
- If $\mathbb{F}$ is a finite field, then the order of $\mathbb{F}$ is a prime power, i.e., $p^n$ where $p \in \textrm{Primes}$ and $ n \geq 1 $.
- Therefore, the order of a finite field is either prime ($p^1$), or the power of a prime ($p^n$ for all $n > 1$).
- Converseley, for every prime power $ q=p^n $ there is a finite field of order $ q $, which is unique (up to relabeling of the elements).
- For $ q = p^n $ with $p \in \textrm{Primes}$, we let $\mathbb{F}_q$ denote the (unique) field of order $ q $. We call $ p $ the characteristic of $\mathbb{F}_q$.
Examples of finite fields¶
Prime field:
- The set $\{0,\dots,p-1\}$, where $p \in \textrm{Primes}$, under addition and multiplication modulo $ p$ is called a prime field $\mathbb{F}_p$. It is the field of residue classes modulo $ p $ written as $ a \equiv b \pmod{p} $. A prime field is of order $ p $. Adding $ p $ copies of any element always results in $ 0 $. The characterisitc of this field is $ p $.
- The elements of $\mathbb{F}_p$ are integers
- $\mathbb{F}_p$ can also be called the ring of integers modulo $ p $
- $\mathbb{F}_p^*$ means all elements of the field without the $0$.
- When $ p = 2 $ in $\mathbb{F}_p $, also noted as $ \texttt{GF}(2)$, addition and substraction is XOR and multiplication is AND. Since the only invertible element is $ 1 $, division is the identity funcction.
Examples of finite fields¶
- For $q=p^n$ where $n > 1$ the set $\{0, . . . , q − 1\}$ is not a field under addition and multiplication modulo $q$. For example, if we take $ q = 3^2 = 9$ then the element $3$ does not have a multiplicative inverse modulo $9$ in this set.
p=11; assert p in P,"p not prime"
Fp = Integers(p) # define field as integers mod p in sage
print(f"Fp_order = {Fp.order()} Fp_characteristic = {Fp.characteristic()} Fp_modulus = {Fp.modulus()} \nFp = {Fp.list()}")
Fp
Fp_order = 11 Fp_characteristic = 11 Fp_modulus = x + 10 Fp = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Ring of integers modulo 11
Fp = GF(p) # define field as finite field in sage
# Fp = FiniteField(p) # alias of GF()
print(f"Fp_order = {Fp.order()} Fp_characteristic = {Fp.characteristic()} Fp_modulus = {Fp.modulus()} \nFp = {Fp.list()}")
Fp
Fp_order = 11 Fp_characteristic = 11 Fp_modulus = x + 10 Fp = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Finite Field of size 11