RSA¶
References:
- [GCAC] A Graduate Course in Applied Cryptography, Dan Boneh and Victor Shoup
- [CINTA] A Computational Introduction to Number Theory and Algebra, Victor Shoup
- [HAC] Handbook of Applied Cryptography, Alfred J. Menezes, Paul C. van Oorschot and Scott A. Vanstone
- [ITMC] Introduction to Modern Cryptography, Jonathan Katz and Yehuda Lindell (3rd Edition)
- Elementary number theory in sage
Dependencies:
This notebook uses sage math as kernel
import sage.misc.banner # sage math version info
rchars = "┘─│┐┌└"
smallbanner = sage.misc.banner.banner_text(full=True)
for c in rchars:
smallbanner = smallbanner.replace(c,"") # remove ascii art box
print(smallbanner)
#banner() # full banner with box
SageMath version 9.5, Release Date: 2022-01-30 Using Python 3.10.12. Type "help()" for help.
RSA - Rivest Shamir Adelman¶
- Rivest Shamir Adelman (RSA) - Adi Shamir, Ron Rivest, Leonard Adelman (all MIT at that time)
- Algorithm first published 1977 "A Method for Obtaining Digital Signatures and Public-key Cryptosystems" ($\approx$28 K citations)
- since 1969 the British signals intelligence GCHQ knew about public-key cryptography (first RSA then DH like)
- Key (modulus) length of $ 2048$ bits still considered secure [ref]

Trapdoor function¶
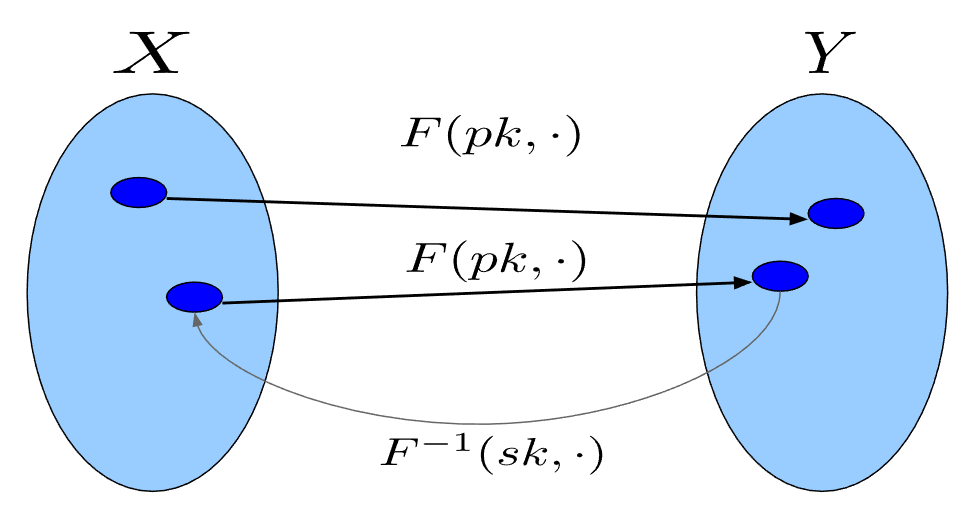
A trapdoor function is a triple of efficient algorithms $\langle G,F,F^{-1} \rangle$ where:
- $G()$ is a key generation algorithm that outputs $(pk,sk)$
- $F(pk,\cdot)$ the $pk$ defines a mapping function $X \to Y$
- $F^{-1}(sk,\cdot)$ defines a function $Y \to X$ that inverts $F(pk,\cdot)$
It holds that $\forall(pk,sk)$ that are the output of $G()$: $$ \forall x \in X: F^{-1}(sk, F(pk,x)) = x $$ Note: If both sets are equal ($X = Y$) then then it is a trapdoor permutation. A secure trapdoor function/permutation is hard to revert without the trapdoor $sk$
Trapdoor permutation¶
Note that there are few (widely believed) trapdoor permutations
- RSA familiy of trapdoor permutations (this slide deck)
- Rabin/Williams squaring permutation on quadratic residues modulo a Blum integer
Trapdoor function¶
RSA - Trapdoor permutation¶
The RSA trapdoor permutation is a triple of efficient algorithms $\langle G,F,F^{-1} \rangle$
- $G()$ key generation function:
- Choose two random primes $p,q$ of at least $ 1024 $ bit each and compute the $ 2048 $ bit modulus $n =pq $
- Choose integers $e,d$ such that $e\cdot d = 1 \pmod{\varphi(n)}$
- There are some commonly used values for $ e $ such as $ e = 3 $ or $ e = 2^{16} + 1 = 65537$
- Output $pk = (n,e)$ and $sk=(n,d)$
- The variabel $ e $ is called the encryption exponent and $ d $ is called the decryption exponent.
- $F(pk,x) = x^e \pmod{\mathbb{Z}_n}$
- This trapdoor permutation defines a mapping between all invertable elements $\mathbb{Z}_n^* \to \mathbb{Z}_n^*$
- $F^{-1}(sk,y) = y^d \pmod{\mathbb{Z}_n}$
- This is the inverse trapdoor permutation
RSA - Security¶
- Computing $\varphi(n)$ without knowing the factorization of $ n $ is the difficulty of computing $ d $
- This is refered to as the RSA problem, which can be solved by factoring $ n $ and computing $\varphi(n) = (p-1)(q-1)$
- Knowing $\varphi(n)$, the multiplicative inverse of $ e $ can be calculated efficiently e.g., with using the extended euclidean algorithm $$ \begin{align*} \varphi(n) &= (p-1)(q-1)\\ e\cdot e^{-1} &=1 \pmod{\varphi(n)}\\ d&:= e^{-1} \pmod{\varphi(n)} \end{align*} $$
# computing multiplicative inverse in python if phi(n) known
def modular_inverse(e, phi_n):
return pow(e,-1,phi_n)
Textbook/raw RSA implementation (insecure)¶
This textbook implementation of RSA is insecure, but we will use it to demonstrate a couple of security issues which have to be addressed when RSA should be used in a secure way.
def rsa_gen(bits=2^1024,_p=None,_q=None,e=None,verbose=False):
proof = (bits <= 2^1024) # turn off time consuming proof for large values
if ( _p and _q ) and _p in Primes() and _q in Primes():
p = _p
q = _q
else:
p = random_prime(bits, proof=proof)
q = random_prime(bits, proof=proof)
if p==q: return None
n = p * q
phi_n = (p-1) * (q-1)
if not e:
while True:
e = ZZ.random_element(1,phi_n)
if gcd(e,phi_n) == 1: break # e has an inverse mod phi_n
d = inverse_mod(e,phi_n)
if verbose: print(f"n = {n}\ne = {e}\nd = {d}\np = {p}\nq = {q}")
return n,e,d,p,q
def rsa_enc(n,e,m):
return pow(m,e,n)
def rsa_dec(n,d,c):
return pow(c,d,n)
def str_to_num(s,n):
""" Function to encode a string as number sequence of their 8 bit ASCII codes """
s = str(s)
if len(s) > floor(log(n,256)):
print("String larger than what can be handled in one rsa invocation")
return None
num = 0
for i in range(len(s)):
num += ord( s[i] )*256**i
return num
def num_to_str(num):
""" Function to decode a number into 8 bit sequences of ASCII characters """
num = Integer(num)
v = []
while num != 0:
v.append(chr( num % 256 ))
num //= 256 # this replaces num by floor(num/256)
return ''.join(v)
Example invocation¶
n,e,d,p,q = rsa_gen(bits=768,verbose=False)
A_as_num = str_to_num("A",n); hex(A_as_num)
'0x41'
AA_as_num = str_to_num("AA",n); hex(AA_as_num)
'0x4141'
num_to_str(A_as_num)
'A'
num_to_str(AA_as_num)
'AA'
Raw RSA - Exampel (insecure)¶
- Lets pick some primes $p=2$ and $q=11$ and compute $n = pq = 22$
- Compute $\varphi(n) = (p-1)(q-1) = 10$
- Find some $e$ such that:
- It is relatively prime to $\varphi(n)$, i.e., $\gcd(e,\varphi(n))=1$
- There is a $d$ such that $e\cdot d = 1 \pmod{\varphi(n)}$
- For our example set $ e = 3 $ and $ d = 7 $, i.e., $ 3 \cdot 7 = 1 \pmod{\varphi(n)}$
- Publish $ pk = (n,e) = (22,3) $ and store $ sk = (n,d) = (22,7) $
- Encryption: of message $ m = 8 $ $$ c = m^e \pmod n = 8^3 \pmod{22} = 512 \pmod{22} = 6 $$
- Decryption: of ciphertext $ c = 6 $ $$ m = c^d \pmod n = 6^7 \pmod{22} = 279936 \pmod{22} = 8 $$
n,e,d,_,_ = rsa_gen(bits=None,_p=2,_q=11,e=3,verbose=True)
n = 22 e = 3 d = 7 p = 2 q = 11
rsa_enc(22,3,8)
6
rsa_dec(22,7,6)
8
Raw RSA - Parameters (p,q) too small¶
If $p$ and $q$ are to small $n$ can be factorized:
n,e,d,_,_ = rsa_gen(bits=None,_p=2,_q=11,e=3,verbose=True) # Alice
n = 22 e = 3 d = 7 p = 2 q = 11
n=22; e=3 # Attacker uses pk of Alice
factor(n) # factors n into its prime factors
2 * 11
phi_n=(2-1)*(11-1); phi_n # computes phi with known factors
10
d=inverse_mod(e,phi_n);d # compute secret key by inverting e
7
Factorization examples¶
n,e,d,p,q = rsa_gen(bits=2^32,e=None,verbose=True) # 2 x 2**32 bit primes
n = 7402481760414978871 e = 6135284656743248681 d = 5889344396117775513 p = 2765346593 q = 2676873047
%time factor(n)
CPU times: user 1.35 ms, sys: 266 µs, total: 1.62 ms Wall time: 1.62 ms
2676873047 * 2765346593
%time euler_phi(n)
CPU times: user 2.24 ms, sys: 442 µs, total: 2.68 ms Wall time: 3.67 ms
7402481754972759232
Factorization examples¶
%time factor(random_prime(2**32)*random_prime(2**32)) # 64 bit n
CPU times: user 1.05 ms, sys: 207 µs, total: 1.26 ms Wall time: 1.3 ms
1096185667 * 3408928543
%time factor(random_prime(2**64)*random_prime(2**64)) # 128 bit n
CPU times: user 30 ms, sys: 285 µs, total: 30.2 ms Wall time: 30.1 ms
2603931075277770449 * 6761297229444507661
%time factor(random_prime(2**96)*random_prime(2**96)) # 192 bit n
CPU times: user 2.34 s, sys: 4.44 ms, total: 2.35 s Wall time: 2.32 s
24008636431434710713745214899 * 54432099488743045962899587171
%time factor(random_prime(2**128)*random_prime(2**128)) # 256 bit n
CPU times: user 3min 6s, sys: 1.05 s, total: 3min 7s Wall time: 3min 4s
236593518623236086418014039105039289109 * 254117808712772563877085158843332102459
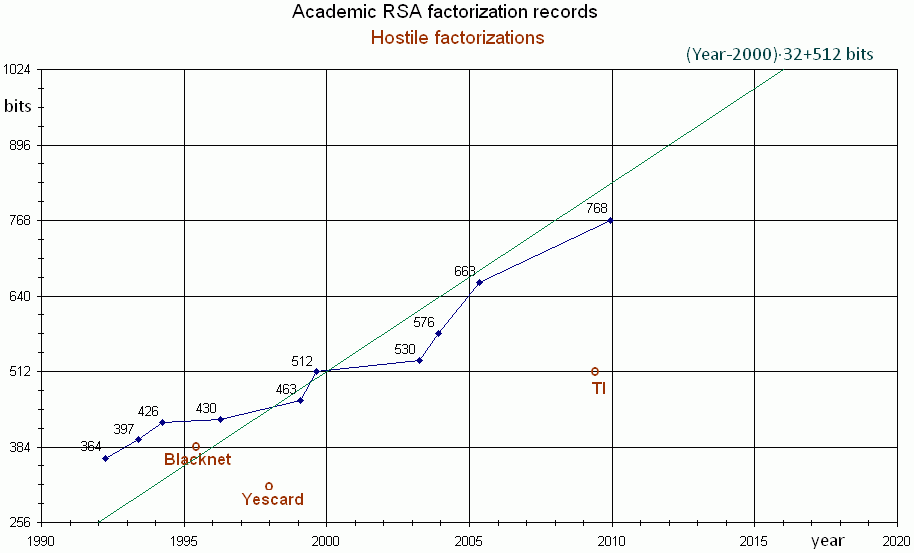
RSA factoring challenge¶
In 1991 the RSA Factoring Challenge (wikipedia) was put forward by RSA Labs, which published a list of semiprimes (numbers which are a product of two primes) and promised rewards for factoring them. Still open challenges left.
- 2019: 795-bit was factored
- 2020: 829-bit was factored
- ...
%time factor(random_prime(2**1024)*random_prime(2**32))
CPU times: user 6.76 s, sys: 17.4 ms, total: 6.77 s Wall time: 6.72 s
2723519431 * 21983046417287773796180412283719780675776530754227844586343094301416162892780538224972896073733307100145410220940906045810591756277080278211068802051726468985140864567899163158808874645764241248922371346185009253002699413538268424645945248436461000566974448734725030893740097344829386540813975326641428678919
%time factor(random_prime(2**2048)*random_prime(2**32))
CPU times: user 51 s, sys: 63.3 ms, total: 51.1 s Wall time: 50.9 s
191055671 * 26104404363605316156687119569868704325729224130602090096059956367020884471442829282631643167244418941044826586676196616763190239932885047564911363831168647439130471107137598125726290464894939054198128947707799135510187559190745168921941096609602843822662534721675483587158404863483846156219346020889559501244976654854463698352831992607139320311264902996593192507315361718701940739609067921951414727881587151800506882077341029531308190944764002232994913856875122606443703942157368357500339742013383626180316817399664817553981658937551290105788412029775012250186539241128350989521849110986247342157214904620430205501523
$p$ and $q$ must be approximately the same size¶
Increasing the number of prime factors is also not a good idea:
bits=32
8*bits
256
%time factor(random_prime(2**bits)*random_prime(2**bits)*random_prime(2**bits)\
*random_prime(2**bits)*random_prime(2**bits)*random_prime(2**bits)\
*random_prime(2**bits)*random_prime(2**bits))
CPU times: user 101 ms, sys: 6 µs, total: 101 ms Wall time: 100 ms
695964457 * 1268842459 * 1299995251 * 1769042687 * 2198083049 * 3011816009 * 3659848187 * 3854359099
Raw RSA: (now assume large $p$ and $q$, other problems?)
- Lets pick some primes $p$ and $q$ and compute $n = pq $
- Compute $\varphi(n) = (p-1)(q-1) $
- Find some $e$ such that:
- It is relatively prime to $\varphi(n)$, i.e., $\gcd(e,\varphi(n))=1$
- There is a $d$ such that $e\cdot d = 1 \pmod \varphi(n)$
- Publish $ pk = (n,e) $ and store $ sk = (n,d) $
- Encryption: of message $ m = 8 $
- $ c = m^e \pmod n $
- Decryption: of ciphertext $ c = 6 $
- $ m = c^d \pmod n $
Raw RSA - Data patterns visible¶
Raw RSA is deterministic encryption, the same plain text leads to the same ciphertext. Moreover, since the public key $pk$ of Alice is public, an attacker can create a dictionary of common values.
Alice <----- E(n,e,"all good") ----- Bob
Alice <----- E(n,e,"error") -------- Bob
n,e,d,p,q = rsa_gen(bits=2^1024,e=65537,verbose=False)
num = str_to_num("error",n)
c = rsa_enc(n,e,num); str(c)[0:50] + "..." # always the same c under (n,e)
'16437021152372803354106913952524123751969881361156...'
m_num = rsa_dec(n,d,c); m = num_to_str(m_num); m
'error'
Raw RSA - Integrity not ensured¶
The integrity of the ciphertext is not ensured. Therefore, the ciphertext is malleable.
n,e,d,_,_ = rsa_gen(bits=2**1024,e=65537)
c = rsa_enc(n,e,8); c # small message from Bob e.g., sensor value
1025290013408837755255130605514510502048030802465163007701667270269652988206056848657038874610326405953470420614549112977624743020313347774663431186056792126711498148234994231057065448464738538484214653069946270845506281357195852516516817514139334810075748696492283823327600836582500958993787424215290226150922733755150933308828996466001555105470849925437344171815734899004752704884149679140256463488614061937960723678479271321352195080830923272282976011253718224980647274960757877077307401385299954404536746008547132054475330629642394983970078161865753146530091888012710099002347620625010676097479229110075352737521
m = rsa_dec(n,d,c); m # Alice decrypts c
8
m = rsa_dec(n,d,c); m # Alice decrypts c
8
c1 = c*c # MitM attacker just multiplies the value with itself
m = rsa_dec(n,d,c1); m # Alice decrypts c1
64
m == 8*8
True
c2 = c*rsa_enc(n,e,2) # MitM attacker can calc. factor using pk
m = rsa_dec(n,d,c2); m # Alice decrypts c2
16
m == 8*2
True
Raw RSA - $e^{th}$ root attack on small $m$¶
If $m$ is small $m < n^{1/e}$ and $ e $ is small, e.g., $e = 3$ and $ m^e < n $, then you can simply calculate the eth root ($\sqrt[e] m$) within the set of integers and decrypt the ciphertext
n,e,d,_,_ = rsa_gen(bits=2**1025,e=3,verbose=True)
n = 497971730645974838681029006423427090725241300976658155717199718178997529991216805349539209461719568284588626766068379735834784827635924398109119587602876134492806897458361917412365944288300721253065686740528877797207779333908248623416276518504678896281961268128247605399915028863192996181436725188084333013641175400011748085980356433723082998139135562738231881003774047339646397760097841585513005347271551447265927375487034217393976507465265775488315294590679783444073694637649897817795174779369990906390998526996772469253560755409656011473269414894989151853463968061623370966765198060616659094665859813934027360719 e = 3 d = 331981153763983225787352670948951393816827533984438770478133145452665019994144536899692806307813045523059084510712253157223189885090616265406079725068584089661871264972241278274910629525533814168710457827019251864805186222605499082277517679003119264187974178752165070266610019242128664120957816792056222008903547224051466072365480391263099312925416950614740981087743491077965146743303531794955288325229901526576621085936577803351294223597358060055173624369876967183389795242532721516555301383740774871460940017259076910495893985775534832034787013332047086253037279063754321954802283656627092893641677976869636275931 p = 284101770455481211181031431071301028608802116790453441192660568887666495681659797442765853033748044227523488309644820921864674349274246239890017212272286933868702331900503952528358909853657310280654041241250692639228662869337695574719140103529724584067161353249344119737076843506778958171560258768363892518307 q = 1752793479067766251104415757133000142208020025666968179498241835032181963482746450314219825678654929877507436937346590502360822794982445515537645763577398800286669873346863014603312850101518318545547259857464464281056907408658188701948791367193938406746696216647768297484929068897061582643084080265680428517
num = str_to_num("A",n); num; hex(num)
'0x41'
c = rsa_enc(n,3,0x41); c # Bob encrypts message m=65 for Alice
274625
hex(274625.nth_root(3)) # Attacker can compute plaintext
'0x41'
Other RSA gotchas¶
Over the years a lot of attacks against RSA have been studied. This shows that getting it right in practise is non-trivial
- Coppersmith attack
- Low encryption exponent $ e $ and small message $ m $
- Or partial knowledge of secret key
- Wiener's attack
- Low decryption exponent $ d $
- Hastad's broadcast attack
- Same message to different public key (moduli) with same (small) $ e $
- Meet in the middle attack
- If small (e.g., 128 bit) non padded value is transferred that is the product of two (e.g., 64 bit) values
- Common factor attacks across multiple keys
- Same prime factors in different moduli
- Mining your p's and q's
- Side channels
- e.g., timing, power consumption, ...
- ...
RSA but how?¶
In general: If alternatives are available better use them. RSA is just a trapdoor permutation and should never be used directly as encryption system (textbook RSA). It has to be embedded/transformed before usage, e.g., OAEP, PKCS1v2.0, or ISO 18033-2
ISO 18033-2 standard roughly:
- $(E_s,D_s)$: Symmetric encryption/ decryption system which provides authenticated encryption
- $H(): \mathbb{N}_n \to K $: Secure hash function that maps elements of $\mathbb{Z}_n $ to secret keys from a symmetric encryption/decryption system
- $G():$ Generate RSA parameter $pk = (n,e)$, $sk = (n,d)$
- $E(pk,m)$: choose random $x$ in $\mathbb{Z}_n$
- $y \gets x^e \pmod{\mathbb{Z}_n}$, and $ k \gets H(x)$, also padding is applied
- output and send $(y,E_s(k,m))$
- $D(sk,(y,c))$: $m = D_s(H(y^d \pmod{\mathbb{Z}_n}),c)$